Algorithm Design Manual:

Reductions are operations that convert one problem into another

An algorithmic problem is a general question with parameters for input and conditions on what makes for a satisfactory solution. An instance is a problem with the input parameters specified.

Example: Problem: The Traveling Salesman Problem (TSP)
Input: A weighted graph G
Output: Which tour {v₁, v₂,...v_n} minimizes ?

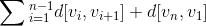Any weighted graph defines an instance of TSP. Each instance has at least one minimum cost tour. The general traveling salesman problem asks for an algorithm to find the optimal tour for all possible instances.

Bandersnatch(G)
    Translate the input G to an instance Y of Bo-Billy Problem
    Call the subroutine Bo-Billy on Y to solve Bandersnatch(G)
    Bandersnatch(G) = Bo-Billy(Y)

Take Home:

Reductions are a way to show that two problems are essentially identical. A fast algorithm (or lack of one) for one of the problems implies a fast algorithm (or lack of one) for the other.

A translation of instances from one type of problem to instances of another such that the answers are preserved is what is meant by a reduction.

Decision Problems

Class of problems whose answers are restricted to true and false are known as decision problems.

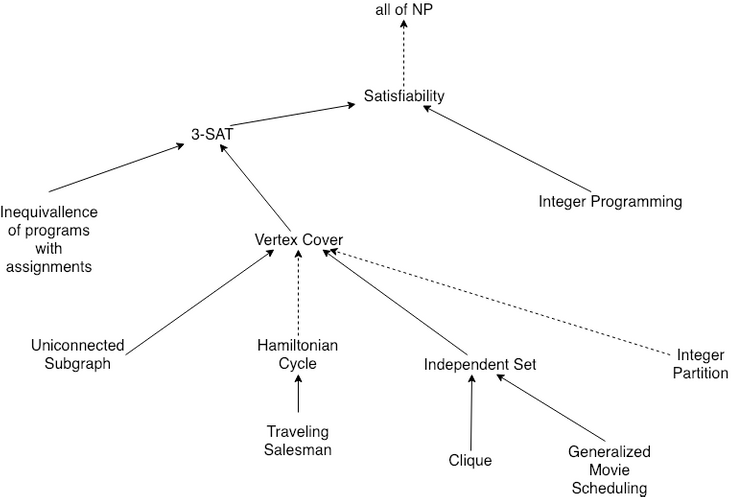
Portion of reduction tree for NP Complete Problems - solid lines are reductions covered in chapter

Art of Proving Hardness

• Make source problem as simple (i.e., restricted) as possible
• Make your target as hard as possible
• Select the right problem for the right reason
• Amplify penalties for making undesired selections
• Think strategically at a high level, then build gadgets to enforce tactics
• When you get stuck, alternate between looking for an algorithm or a reduction

Take Home:

Approximation algorithms guarantee answers that are always close to the optimal solution. They can provide a practical approach to dealing with NP-complete problems.

Note from Note-Taker:

This chapter was very math-based and I skipped over the majority of it.