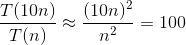Computer Science Distilled
Chapter Two
Complexity
2019-01-30
Time complexity is written T(n) and gives the number of operations performed when processing input of size n - we also refer to it as "running cost". If a function is quadratic (n2), we can predict how much longer it takes to run with double the input using
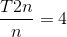
When an algorithm can have different values of T(n) for the same value of n, we use cases:
- Best Case - When input requires minimum number of operations for any input of that size. For sorting, this is usually the case for already sorted input.
- Average Case - Average number of operations for input of a given n. For sorting, an input in random order is usually considered.
- Worst Case - When input requires maximum number of operations for input of a given size. In many sorting algorithms, that's when the input is given in reverse order.
In general, we care about the worst case. This gives a guaranteed baseline that we can count on.
2.1 Counting Time
Let's use Selection Sort as an example for how to calculate time complexity. In Selection Sort, an outer loop updates the current position being sorted and an inner loop selects the items that goes in the current position
function selection_sort(list)
for current <- 1 ... list.length - 1
smallest <- current
for i <- current + 1 ... list.length
if list[i] < list[smallest]
smallest <- i
list.swap_items(current, smallest)The outer loop runs n - 1 times and does two operations per run (one assignment and one swap), totalling 2n - 2 operations. The inner loop first runs n - 1 times, then n - 2 times, then n - 3 times, etc.
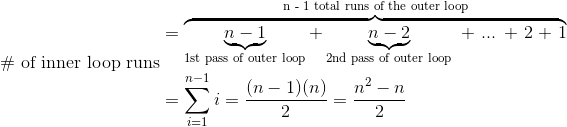
In the worst case, the if condition is always met, so the inner loop does one comparison and one assignment (n2 - n)/2 times, hence n2 - n operations. The algorithm costs 2n - 2 operations for the outer loop and n2 - n for the inner loop. Because constants are ignored, the time complexity is T(n) = n2 + n - 2. In terms of Big O, we can round to n2 because n2 is the dominant term.
Understanding Growth
To predict how execution time will grow, you don't need to know all the terms of T(n). You can approximate by taking the fastest-growing or dominant term.
Index Cards:
Problem: Yesterday, you spilled a box of index cards and it took you two hours of sorting to put the items in the correct order. Today, you knocked over 10 boxes. How much time do you need to fix your greivous error?
2.2 Big O Notation:
Big O Notation is a special notation referring to the classes of growth and is used for expressing the dominant term of an algorithm cost function in the worst case.
When designing, it's important to anticipate the most frequent operations necessary to your algorithm and to figure out the best data structure to use that may minimize the cost of such operations.
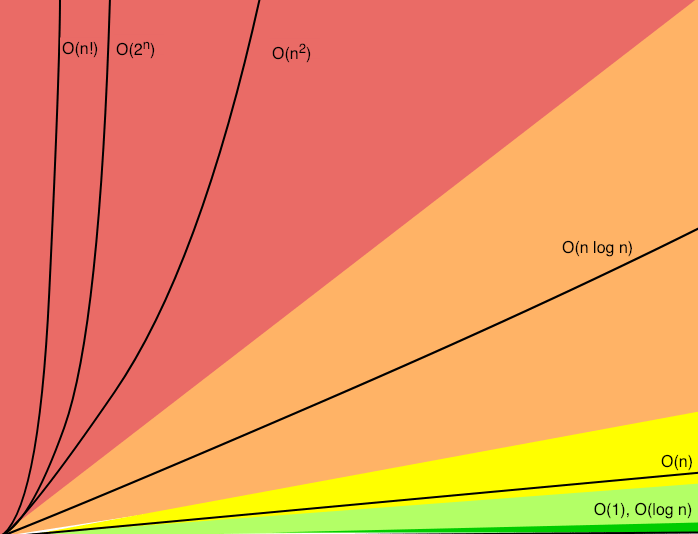
Graph I made to represent some Big O notations
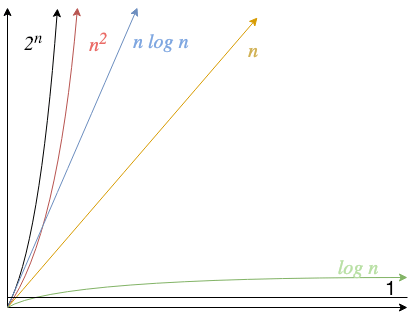
2.3 Exponentials:
O(2n) is known as exponential time. Functions written in exponential time grow so quickly, they're considered not runnable as they work for few input types and require a lot of computing power if inputs aren't tiny.
Some algorithms are worse even than exponential, such as factorial time algorithms (n!).
2.4 Counting Memory
The measurement of the amount of working storage an algorithm needs is called space complexity. We measure space complexity in much the same way we measure time complexity, but count memory rather than computing operations. Usually have to make a trade off between have a good space complexity or having a good time complexity.