Programming Foundations:
Algorithms
2018-11-21
Algorithm Characteristics:
Algorithm complexity
Space complexity - How much memory does it require?
Time complexity - How much time does it take to compute?
Inputs and output - What does the algorithm accept? What does it return?
Classification:
- serial (sequential)
- parallel (breaks dataset into pieces and works on them simultaneously)
- exact (produces a known predictable answer)
- approximate (tries to find answer that may or may not be exact)
- deterministic (executes each step with an exact decision)
- non-deterministic (attempts to get to solution through successive guesses that get better over time)
Common Algorithms
Search - Find specific data in a structure
Sorting - Take dataset and put it in order
Computational algorithms - Given a set of data, calculate another (ex: is a given number prime?)
Collection algorithms - Work with collections of data (count specific items, navigate among data elements, filter out unwanted data, etc.)
Euclid's Algorithm
Find the greatest common denominator of two integers (largest integer that divides both with no remainder):
Example: GCD of 20 and 8 is 4 (because 8 / 4 is 2 and 20 / 4 is 5)
- For two integers a and b, where a > b, divide a by b
- If the remainder, r, is 0, then stop - GCD is b.
- Otherwise, set a to b, b to r, and repeat at step 1 until r is 0.
GCD (20, 8) | a | b | r | |----|---|---| | 20 | 8 | 4 | | 8 | 4 | 0 |
Find the greatest common denominator of two numbers using Euclid's algorithm
def gcd(a, b):
while (b != 0):
t = a
a = b
b = t % b
return aTry out the function with a few examples
print(gcd(60, 96)) // should be 12
print(gcd(20, 8)) // should be 4Understanding Algorithm Performance
Measure how an algorithm responds to dataset size Big-O Notation:
- Classifies performance as the input size grows
- "O" indicates the order of operation: time scale to perform an operation Many algorithms and data structures have more than one O value
- Inserting data, searching for data, deleting data, etc.
Common Big-O Terms
Notation Description Example O(1) Constant Time Looking up a single element in an array O(log n) Logarithmic Finding an item in a sorted array with a binary search O(n) Linear time Searching an unsorted array for a specific value O(n log n) Log-linear Complex sorting algorithms like heap sort and merge sort O(n^2) Quadratic Simple sorting algorithms, such as bubble sort, selection sort, and insertion sort
Data Structures
Data structures are used to organize data so it can be processed
Common Data Structures
- Arrays
- Linked lists
- Stacks and queues
- Trees
- Hash tables
Arrays
Collection of elements identified by index or key Linear set of values Element positions can be calculated using a mathematical expression
- Allows elements to be accessed in random access fashion Arrays in most languages start index at 0
Array Operations
Calculate item index: O(1) Inserting or deleting item at beginning: O(n) Inserting or deleting item in middle: O(n) Inserting or deleting at the end: O(1)
Linked List
Linear collection of data elements, called nodes Each node has a field that points at the next element in the list Each element can contain data application needs First item in list is called the head Last item has field that points to nothing to indicate it's the end of the list Each item only knows about the next element, unless doubly linked list Doubly-linked lists have references to previous and next Elements can be easily inserted and removed Underlying memory doesn't need to be reorganized Can't do constant-time random item access Item lookup is linear in time complexity
Linked list example
The Node class
class Node(object):
def __init__(self, val):
self.val = val
self.next = None
def get_data(self):
return self.val
def set_data(self, val):
self.val = val
def get_next(self):
return self.next
def set_next(self, next):
self.next = nextThe Linked List class
class LinkedList(object):
def __init__(self, head=None):
self.head = head
self.count = 0
def get_count(self):
return self.count
def insert(self, data):
new_node = Node(data)
new_node.set_next(self.head)
self.head = new_node
self.count += 1
def find(self, val):
item = self.head
while (item != None):
if item.get_data() === val:
return item
else:
item = item.get_next()
return None
def deleteAt(self, index):
if index > self.count-1:
return
if index == 0:
self.head = self.head.get_next()
else:
tempIndex = 0;
node = self.head
while tempIndex < index - 1:
node = node.get_next()
tempIndex += 1
node.set_next(node.get_next().get_next())
self.count -= 1
def dump_list(self):
tempnode = self.head
while (tempnode != Node):
print("Node: ", tempnode.get_date())Create a linked list and insert some items
itemlist = LinkedList()
itemlist.insert(38)
itemlist.insert(49)
itemlist.insert(13)
itemlist.insert(15)
itemlist.dump_list()Exercise the list
print("Item count: ", itemlist.get_count())
print("Finding item: ", itemlist.find(13))
print("Finding item: ", itemlist.find(78))Delete an item
itemlist.deleteAt(3)
print("Item count: ", itemlist.get_count())
print("Finding item: ", itemlist.find(38))
itemlist.dump_list()Stacks and Queues
Stack - collection that supports push and pop operations
- The last item pushed is the first one popped Pushing a value onto the stack is a constant time operation Removing from stack is also constant time
Queue - collection that supports adding and removing
- First item added is the first item out
Practical Applications
Stack
- Expression processing (like Polish notation)
- Backtracking: browser and back button, for example
Queue
- Order processing
- Message processing
Stack Example
Create a new empty list that we'll use as a stack
stack = []Put items onto the stack
stack.append(1)
stack.append(2)
stack.append(3)
stack.append(4)Print the stack contents
print(stack) // [1, 2, 3, 4]Pop an item off the stack
x = stack.pop()
print(x)
print(stack)Queue Example
Python deque is optimized for adding and removing elements from both ends of the collection.
from collections import deque
Create an empty deque object that will function as a queue
queue = deque()Add some items to the queue
queue.append(1)
queue.append(2)
queue.append(3)
queue.append(4)Print the queue contents
print(queue)Pop an item off the front of the queue
x = queue.popleft()
print(x)
print(queue)Hash Tables
Form of associative array that maps keys to their associated values using hash function Hash function uses key to compute an index into the slots that are in the hash table and map the key to the value. Ideally, hash function will assign each key to a unique slot in the table where the values are stored. In reality, sometimes there are collisions where two separate keys map to the same slot in the table. In those cases, the hash table needs to have a way of resolving those collisions so the correct value is mapped to the correct key. Most languages and frameworks have hash table data structures figured out for you already
Advantages
Key-to-value mappings are unique Hash tables are typically very fast
Drawbacks
For small datasets, arrays are usually more efficient Hash tables don't order entries in a predictable way
Hash Table Example
Create a hashtable all at once
items1 = dict({"key1": 1, "key2": 2, "key3": "three"})
print(items1) // {'key3': 'three', 'key2': 2, 'key1': 1}Create a hashtable progressively
items2 = {}
items2["key1"] = 1
items2["key2"] = 2
items2["key3"] = 3
print(items2) // {'key3': 3, 'key2': 2, 'key1': 1}Try to access a nonexistant key
print(items1["key6"]) // Throws an exceptionReplace an item
items2["key2"] = "two"
print(items2) // {'key3': 3, 'key2': 'two', 'key1': 1}Iterate the keys and values in the dictionary
for key, value in items2.items():
print("Key: ", key, " value: ", value)
# ('Key: ', 'key3', ' value: ', 3)
# ('Key: ', 'key2', ' value: ', 'two')
# ('Key: ', 'key1', ' value: ', 1)Recursion
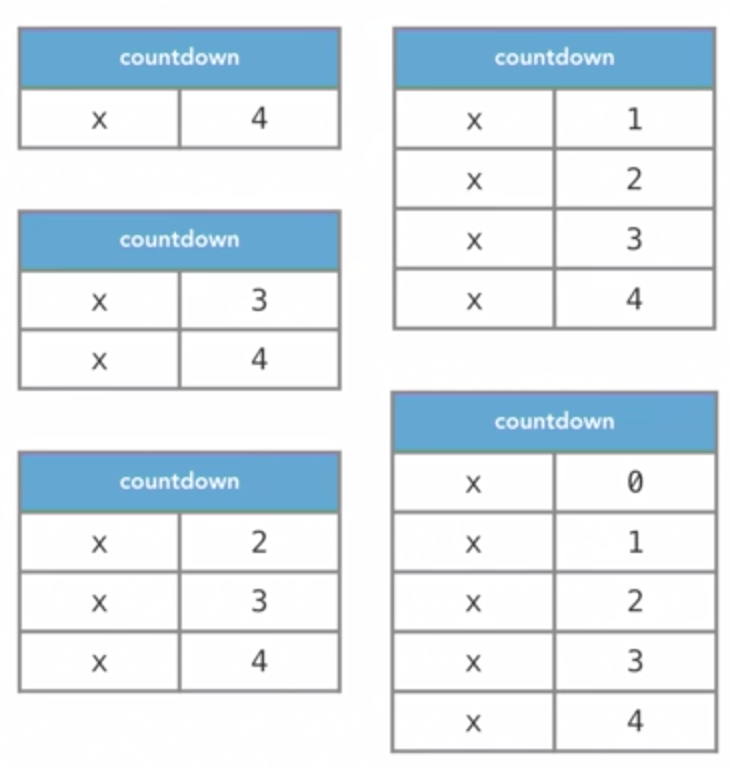
Recursion is when a function calls itself
Important things to remember:
Recursive functions need to have a breaking condition
- This prevents infinite loops and eventual crashes
Each time the function is called, the old arguments are saved
This is called the "call stack"
Recursion Example
function countdown(x) {
if (x == 0)
print("done!")
return
else
print(x, "...")
countdown(x-1)
}
countdown(4)def countdown(x):
if x == 0:
print("Done!")
return
else:
print(x, "...")
countdown(x-1)
print("foo")
countdown(5)
# 5 ...
# 4 ...
# 3 ...
# 2 ...
# 1 ...
# Done!
# foo
# foo
# foo
# foo
# foo# 2^4 = 2*2*2*2 = 16
def power(num, pwr):
if pwr == 0:
return 1
else:
return num * power(num, pwr-1)
# 5! = 5x4x3x2x1 = 20 but 0! = 1
def factorial(num):
if num == 0:
return 1
else:
return num * factorial(num - 1)
print("{} to the power of {} is {}".format(5, 3, power(5, 3)))
print("{} to the power of {} is {}".format(1, 5, power(1, 5)))
print("{}! is {}".format(4, factorial(4)))
print("{}! is {}".format(0, factorial(0)))
/*
Console output:
5 to the power of 3 is 125
1 to the power of 5 is 1
4! is 24
0! is 1
*/Sorting Data
Bubble Sort
Bubble sort compares first two elements to each other to see which is larger.
If the first item is larger than the second, swap
Keep swapping until element in correct place
Go to next index, repeat
Simple to understand and implement
Performance: O(n^2)
- For loops inside for loops are usually n^2 Other sorting algorithms are generally much better
Not considered a practical solution
Bubble Sort Example
def bubbleSort(dataset):
# Start with the array length and decrement each time
for i in range(len(dataset) - 1, 0, -1): // start, stop, step
for j in range(i):
if dataset[j] > dataset[j+1]:
temp = dataset[j]
dataset[j] = dataset[j+1]
dataset[j+1] = temp
print("Current state: ", dataset)
def main():
list1 = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53]
bubbleSort(list1)
print("Result: ", list1)
if __name__ == "__main__":
main()Output in console:
Current state: [6, 8, 19, 20, 23, 56, 41, 49, 53, 87]
Current state: [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]
Current state: [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]
Current state: [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]
Current state: [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]
Current state: [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]
Current state: [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]
Current state: [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]
Current state: [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]
Result: [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]Merge Sort
Divide and conquer algorithm
Breaks dataset into individual pieces and merges them
Uses recursion to operate on datasets
Performs well on large sets of data
In general has a performance of O(n log n)
Steps
Break arrays down into arrays of 1 element Go through and merge arrays together, maintaining sort
Merge Sort Example
items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53]
def mergeSort(dataset):
if len(dataset) > 1:
mid = len(dataset) // 2
leftarr = dataset[:mid]
rightarr = dataset[mid:]
# Recursively break down the arrays
mergesort(leftarr)
mergesort(rightarr)
# Perform the merges
i = 0 # index into the left array
j = 0 # index into the right array
k = 0 # index into the merged array
# While both arrays have content
while i < len(lefarr) and j < len(rightarr):
if leftarr[i] < rightarr[i]:
dataset[k] = leftarr[i]
i += 1
else:
dataset[k] = rightarr[j]
j += 1
k += 1
while i < len(leftarr):
dataset[k] = leftarr[i]
i += 1
k += 1
while j < len(rightarr):
dataset[k] = rightarr[j]
j += 1
k += 1
# test the merge sort with data
print(items)
mergesort(items)
print(items)Output:
[6, 20, 8, 19, 56, 23, 87, 41, 49, 53]
[6, 8, 19, 20, 23, 41, 49, 53, 56, 87]Quicksort
Divide and conquer algorithm
Also uses recursion
Generally performs better than merge sort, O(n log n)
Operates in place
Worst case is O(n^2) when data is mostly sorted already
Procedure
Start by picking a pivot position
Start by incrementing the lower index as long as it's lower than the upper index until you find a value larger than the pivot value
On the right side, you increase until you find a value less than the pivot
Swap element at lower index with element at upper index
When indexes meet, that's the split
Split into two arrays - one that's lower than the pivot and one that's larger than pivot
Quick Sort Example
items = [20, 6, 8, 53, 56, 23, 87, 41, 49, 19]
def quickSort(dataset, first, last):
if first < last:
# calculate the split point
pivotIndex = partition(dataset, first, last)
# now sort the two partitions
quickSort(dataset, first, pivotIndex-1)
quickSort(dataset, pivotIndex+1, last)
def partition(datavalues, first, last):
# choose the first item as the pivot value
pivotvalue = datavalues[first]
# establish the upper and lower indexes
lower = first + 1
upper = last
# start searching for the crossing point
done = False
while not done:
# advance the lower index
while lower <= upper and datavalues[lower] <= pivotvalue:
lower += 1
# advance the upper index
while datavalues[upper] >= pivotvalue and upper >= lower:
upper -= 1
# if the two indexes cross, we found the split point
if upper < lower:
done = True
# otherwise, swap
else:
temp = datavalues[lower]
datavalues[lower] = datavalues[upper]
datavalues[upper] = temp
# when the split point is found, exchange the pivot value
temp = datavalues[first]
datavalues[first] = datavalues[upper]
datavalues[upper] = temp
# return the split point index
return upper
print(items)
quickSort(items, 0, len(items)-1)
print(items)Output:
[20, 6, 8, 53, 56, 23, 87, 41, 49, 19]
[6, 8, 19, 20, 23, 41, 49, 53, 56, 87]Searching for data in an unordered list (Linear Search)
# declare a list of values to operate on
items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53]
def find_item(item, itemlist):
for i in range(0, len(itemlist)):
if item == itemlist[i]:
return i
return None
print(find_item(87, items))
print(find_item(250, items))Searching an Ordered List (Binary Search)
To perform binary search:
- Calculate midpoint of list rounded down
- Check if value we're searching for is at the midpoint
-
If not:
- If number at midpoint is lower than the value searching for, can ignore indexes following it
- Advance upper index to midpoint, calculate new midpoint
- If number at midpoint is higher than the value searching for, can ignore indexes preceding it
- Advance lower index to midpoint, calculate new midpoint
Performance: O(log n)
Example:
items = [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]
def binarysearch(item, itemlist):
# get the list size
listsize = len(itemlist) - 1
# start at the two ends of the list
lowerIndex = 0
upperIndex = listsize
while lowerIndex <= upperIndex:
# calculate the midpoint
midPoint = (lowerIndex + upperIndex) // 2
# if item found, return the index
if itemList[midPoint] == item:
return midPoint
# otherwise, calculate new midpoint
if item > itemList[midPoint]:
lowerIndex = midPoint + 1
else:
upperIndex = midPoint - 1
if lowerIndex > upperIndex:
return None
print(binarysearch(23, items))
print(binarysearch(87, items))
print(binarysearch(250, items))Output:
4
9
NoneExample to determine if a list is sorted
items1 = [6, 8, 19, 20, 23, 41, 49, 53, 56, 87]
items2 = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53]
def is_sorted(itemlis):
# using the brute force method
for i in range(0, len(itemlist)-1):
if (itemlist[i] > itemlist[i+1]):
return False
return True
print(is_sorted(items1))
print(is_sorted(items2))Output:
True
FalsePython Comprehension version
def is_sorted(itemlist):
return all(itemlis[i] <= itemlist[i+1] for i in range(length(itemlist)-1))Filter with Hash Table Example O(n)
# define a set of items that we want to reduce duplicates
items = ["apple", "pear", "orange",
"banana", "apple", "orange", "apple",
"pear", "banana", "orange", "apple",
"kiwi", "pear", "apple", "orange"]
# createa hashtable to perform a filter
filter = dict()
# loop over each item and add to the hashtable
for key in items:
filter[key] = 0
# create a set from the resulting keys in the hashtable
result = set(filter.keys())
print(result)Value Counting with Hash Table O(n)
# define a set of items that we want to count
items = ["apple", "pear", "orange",
"banana", "apple", "orange", "apple",
"pear", "banana", "orange", "apple",
"kiwi", "pear", "apple", "orange"]
# create a hashtable object to hold the items and counts
counter = dict()
# iterate over each item and increment the count for each one
for item in items:
if (item in counter.keys()):
coutner[item] += 1
else:
counter[item] = 1
# print results
print(count)Output:
{'apple': 5, 'pear': 3, 'orange: 4, 'banana': 2, 'kiwi': 1}Find maximum value with recursion
# declare a list of values to operate on
items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53]
def find_max(items):
# breaking condition: last item in list? return it
if len(items) == 1:
return items[0]
# otherwise get the first item and call function again
# to operate on the rest of the list
op1 = items[0]
op2 = find_max(items[1:])
# perform the comparison when we're down to just two
if op1 > op2:
return op1
else:
return op2
# test the function
print(find_max(items)) // 87