Algorithm Design Manual:
Chapter Two
Algorithm Analysis
2019-01-11
Random Access Memory (RAM) Computation Model:
- Each imple operation (x, *, -, =, if, call) takes one time step
- Loops and subroutines take
ntime steps - Each memory access takes one time step
Take-Home Lesson:
Algorithms can be understood and studied in a language and machine-independent manner.
Best, Worst, and Average-Case Complexity
You could represent every possible instance of data to an algorithm on a graph, using the x-axis to represent the size of the input problem and the y-axis to represent the number of steps taken for that instance. We can define three interesting functions over the plot of those points:
-
The
worst-case complexityof the alorithm is the function defined by the maximum number of steps taken in any instance of sizen. This represents the curve passing through the highest point in each column. This is the one we care the most about. -
The
best-case complexityof the algorithm is the function defined by the minimum number of steps taken in any instance of sizen. This represents the curve passing through the lowest point of each column. -
The
average-case complexityof the algorithm, which is the function defined by the average number of steps over all instances of sizen.
The Big Oh Notation
It is difficult to deal directly with the functions of best, worst, and average case because they tend to:
- Have too many bumps
- Require too much detail to specify precisely
Big Oh notation ignores the difference between multiplicative constants. The function f(n) = 2n and g(n) = n are identical in Big Oh analysis. Suppose a given algorithm in C ran twice as fast as one with the same algorithm written in Java. The multiplicative of two tells us nothing about the algorithm itself since both programs implement the same algorithm. We ignore such constant factors when comparing two algorithms.
Formal definitions associated with the Big Oh notation are as follows:
-
f(n) = O(g(n)) means c . g(n) is an upper bound on f(n). Thus there exists some constant c such that f(n) is always <= c . g(n) for large enough n (i.e., n >= n0 for some constant n0).
-
f(n) = Ω(g(n)) means c . g(n) is a lower bound on f(n). Thus there exists some constant c such that f(n) is always >= c . g(n) for all n >= n0.
-
f(n) = ϴ(g(n)) means c1 . g(n) is an upper bound on f(n) and c2 . \g(n)_ is a lower bound on f(n), for all n >= n0. Thus there exist constants c1 and c2 such that f(n) <= c1 . g(n) and f(n) >= c2 . g(n). This means that g(n) provides a nice, tight bound on f(n).
Take-home Lesson:
The Big Oh notation and worst-case analysis are tools that greatly simplify our ability to compare the efficiency of algorithms.
Says to work through these examples, but I won't:
-
3n2 - 100n + 6 = O(n2), because I choose c = 3 and 3n2 > 3n2 - 100n + 6;
-
3n2 - 100n + 6 = O(n3), because I choose c = 1 and n3 > 3n2 - 100n + 6 when n > 3;
-
3n2 - 100n + 6 ≠ O(n), because for any c I choose c x n < 3n2 when n > c;
-
3n2> - 100n + 6 = Ω(n2), because I choose c = 2 and 2n2 < 3n2 - 100n + 6 when n > 100;
-
3n2 - 100n + 6 ≠ Ω(n3), because I choose c = 1 and 3n2 - 100n + 6 < n3 when n > 3;
-
3n2 - 100n + 6 = Ω(n), because for any c I choose cn < 3n2 - 100n + 6 when n > 100c;
-
3n2 - 100n + 6 = ϴ(n2), because both O and Ω apply;
-
3n2 - 100n + 6 ≠ ϴ(n3), because only O applies;
-
3n2 - 100n + 6 ≠ ϴ(n), because only Ω applies;
Stop and think: Back to the definition:
Problem: Is 2n+1 = ϴ(2n)?
Solution: All Big Oh problems can be correctly solved by going back to the definition and working with that.
-
Is 2n+1 = O(2n>)? Well, f(n) = O(g(n)) iff (if and only if) there exists a constant that for all sufficiently large n f(n) <= c . g(n). Is there? The key observation is that 2n+1 = 2 . 2n, so 2 . 2n <= c . 2n for any c >= 2.
-
Is 2n+1 = Ω(2n)? Go back to the definition. f(n) = Ω(g(n)) iff there exists a constant c > O such that for all sufficiently large n f(n) >= c .g(n). This would be satisfied for any O < c <= 2. Together the Big Oh and Ω bounds imply 2n+1 = Θ(2n)
Stop and Think: Hip to the Squares?
Problem: Is (x+y)2 = O(x2 + y2)?
Solution:
Working with Big Oh means going back to the definition. By definition, the expression is valid iff we can find some c such that (x+y)2 <= c(x2 + y2).
Dominance Relations:
Big Oh groups functions into classes. Faster-growing functions dominate slower-growing ones. Some classes include:
- Constant functions - f(n) = 1. There is no dependence on the parameter n.
- Logarithmic functions - f(n) = log(n) e.g. binary search. Function grows slowly as n increases but faster than constant
- Linear functions - f(n) = n Functions that measure the cost of looking at every item once (or twice, or ten times) in an n element array
- Superlinear functions - f(n) = n log n e.g. quicksort/merge sort
- Quadratic functions - f(n) = n2 Functions that measure the cost of looking at most or all pairs of items in an n element universe - e.g. insertion sort/selection sort
- Cubic functions - f(n) = n3 Iterate through triples of items in \n_ element universe
- Exponential functions - f(n) = cn for a given constant c > 1. Functions like 2n arise when enumerating over all subsets of n items
- Factorial functions - f(n) = n! Functions that arise when generating all permutations or orderings of n items.
n! >> 2n >> n3 >> n2 >> n log n >> n >> log n >> 1
Adding Functions
The sum of two functions is governed by the dominant one: n3 + n2 + n + 1 = O(n3)
Multiplying Functions
Multiplying a function by another constant does not affect big O - O(c . f(n)) -> O(f(n)) If both functions in a product are increasing, both are important: O(f(n)) * O(g(n)) -> O(f(n) * g(n))
Selection Sort:
Identify smallest unsorted element and place at end of sorted portion
selection_sort(int s[], int n) {
int i, j /* counters */
int min; /* index of minimum */
for (i = 0; i < n; i++) {
min = i;
for (j = i + 1; j < n; j++) {
if (s[j] < s[min]) min = j;
swap(&s[i], &s[min]);
} /* Nested loop runs n - i - 1 times where i is index of outer loop */
} /* Outer loop runs n times */
}The number of times the if statement is executed is given by:
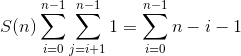
S(n) = (n - 1) + (n - 2) + (n - 3) + ... + 2 + 1
Insertion Sort
for (i = 1; i < n; i++) {
j = i;
while ((j > 0) && (s[j] < s[j - 1])) {
swap(&s[j], &s[j-1]);
j = j - 1;
}
}Even though there are two stopping conditions for the inner loop, we assume it runs n times for worst case since i < n, making insertion sort quadratic - O(n2)
String Pattern Matching
Problem: Substring pattern matching Input: A text string t and a pattern string p Output: Does t contain the pattern p as a substring and if so, where?
int findMatch(char* p, char* t) {
int i, j; /* counters */
int m, n; /* string lengths */
m = strlen(p);
n = strlen(t);
for (i = 0; i <=(n-m); i=i+1) {
j = 0;
while ((j<m) && (t[i+j]==p[j]))
j = j+1;
if (j == m) return(i);
}
return (-1);
}Matrix Multiplication
Problem: Matrix multiplication Input: Two matrices, A (of dimension x . y) and B (dimension y . z) Output: An x . z matrix C where C[i][j] is the dot product of the ith row of A and the jth column of B
for (i = `; i <= x; i++) {
for (j = 1; j <= z; j++) {
C[i][j] = 0;
for (k = 1; k <= y; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}Logarithms
Functions that grow slowly and arise in any process where things are repeatedly halved or doubled. Example: Binary search